
 |
|
|
#1 |
|
Sonsuz Limitler & Dikey Asimptotlar (Infinite Limits & Vertical Asmyptotes)
Bu bölümde limitin +∞ ve −∞ olduğu durumları inceleyeceğiz. Sonraki bölümlerde ve diğer bazı derslerde de karşımıza düzenli olarak çıkan bu limitlerle nasıl başetmemiz gerektiğini Çözümlü Problem Set bölümünde öğreneceksiniz. Sonsuz limitler aslında gerçek limit değildir, fakat değerleri çok büyük olan fonksiyonların davranışlarını tanımlamak için önemli bilgiler sağlar. Sonsuz limit, bir x=a noktasına yaklaştığınızda (sağdan ve/veya soldan) fonksiyonunuzun çok büyük değerler (tatmin olabileceğiniz kadar büyük) aldığını söyler. Bu çok büyük pozitif veya çok büyük negatif değerleri yazmak yerine +∞ ve −∞ kullanırız. Bunu matematiksel olarak aşağıdaki gibi ifade ederiz. [Üye Olmadan Linkleri Göremezsiniz. Üye Olmak için TIKLAYIN...] Dikey (Düşey) Asimptot: Kavramsal olarak Asimptot bir fonksiyonun grafiğinin yaklaştığı çizgi veya eğridir. Dikey (Düşey) Asimptot ise, x-ekseni üzerindeki sabit bir x=a noktasına yaklaşıldığında (x→a) fonksiyonun yaklaştığı dikey çizigidir. Bu noktada i) fonksiyonun alacağı değerin büyüklüğü için bir sınır yoktur ve onu ±∞ ile ifade ederiz, ii) fonksiyon tanımsızdır ve dolayısıyla iii) limiti yoktur. Sonuç olarak aşağıdaki durumlardan en az biri sağlanıyorsa, x=a çizgisi artık fonksiyonun dikey asimpotudur; [Üye Olmadan Linkleri Göremezsiniz. Üye Olmak için TIKLAYIN...] Aşağıdaki şekilde dikey asimptot şematik olarak gösterilmiştir. Ayrıca, herhangi bir fonksiyonun dikey asimptotunu bulmak için uygulanması gereken 3 temel adım özetlenmiştir. 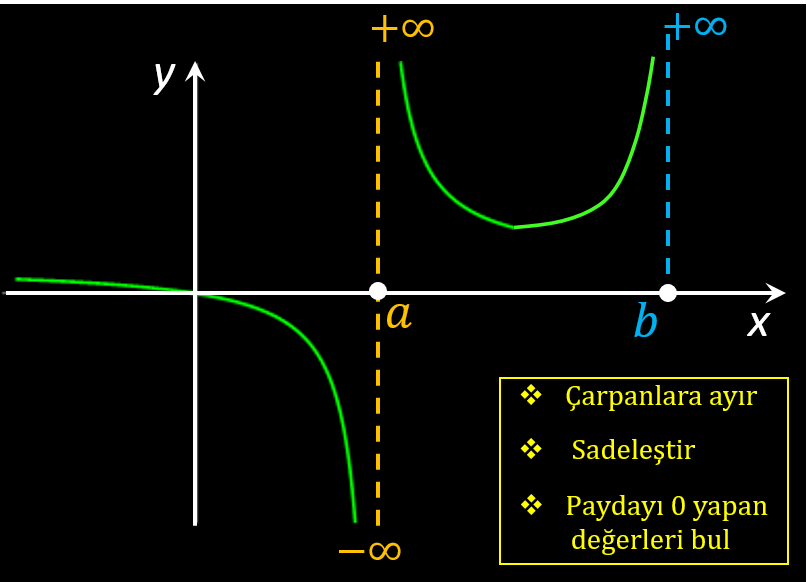 Sonsuz limit ve sonsuzda limit hesaplamarında dikkat edilmesi gereken en önemli unsurlardan biri de ∞− Aritmetiği 'dir. x=a noktasını fonksiyonda yerine koyduktan sonra elde ettiğiniz sonucun tanımlı, tanımsız veya belirsiz olma durumuna göre yol alırsınız. Bu nedenle sonucun hangi durumlarda tanımlı, hangi durumlarda tanımsız ve belirsiz olduğuna karar vermeniz gerekecektir. Aşağıdaki tablo, size bu konuda yol göstermeyi amaçlamaktadır.  alıntı |
|
|
|
| Konuyu Toplam 1 Üye okuyor. (0 Kayıtlı üye ve 1 Misafir) | |
|
|